Naive Bayes classifiers are a family of “probabilistic classifiers” based on Bayes’ theorem with strong independence between the features. They are among the simplest Bayesian network models and are capable of achieving high accuracy levels.
Bayes theorem states mathematically as:
P(A|B) = ( P(B|A) * P(A) )/ P(B)
where A and B are events and P(B) != 0.
P(A|B) is a conditional probability: the probability of event A occurring given that B is true.
P(B|A) is also a conditional probability: the probability of event B occurring given that A is true.
P(A) and P(B) are the probabilities of observing A and B respectively without any given conditions.
A and B must be different events.
In this post, we will write the program for Naive Bayes Classification. We will use python to write this program and we will not use any libraries.
Input
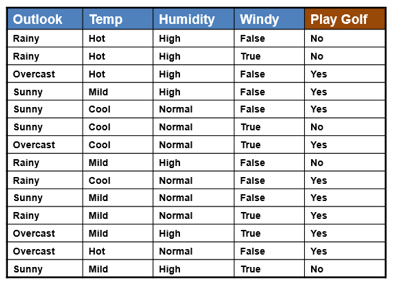
We have the dataset given below. It consists of weather information of the past few days and also whether golf can be played on that day or not.
Converting to list
Now, using the above dataset, we have to predict whether golf can be played on the given weather conditions or not.
For this we will first create convert our dataset into list.
Assigning numbers to the data outlook rainy = 0, overcast = 1, sunny = 2 temperature hot = 0, mild = 1, cool = 2 humidity normal = 0, high = 1 windy false = 0, true = 1 play golf no = 0, yes = 1
#dataset converted to integers using above notations
dataset = [
[0,0,1,0,0],
[0,0,1,1,0],
[1,0,1,0,1],
[2,1,1,0,1],
[2,2,0,0,1],
[2,2,0,1,0],
[1,2,0,1,1],
[0,1,1,0,0],
[0,2,0,0,1],
[2,1,0,0,1],
[0,1,0,1,1],
[1,1,1,1,1],
[1,0,0,0,1],
[2,1,1,1,0]
]Separating the data
Now we have to separate the data according to the Play Golf column (which is ‘y’ since this is what we have to predict). For this, we will create a dictionary and append the list into it.
mp = dict()
for i in range(len(dataset)):
row = dataset[i]
y = row[-1]
if (y not in mp):
mp[y] = list()
mp[y].append(row)
for label in mp:
print(label)
for row in mp[label]:
print(row)0 [0, 0, 1, 0, 0] [0, 0, 1, 1, 0] [2, 2, 0, 1, 0] [0, 1, 1, 0, 0] [2, 1, 1, 1, 0] 1 [1, 0, 1, 0, 1] [2, 1, 1, 0, 1] [2, 2, 0, 0, 1] [1, 2, 0, 1, 1] [0, 2, 0, 0, 1] [2, 1, 0, 0, 1] [0, 1, 0, 1, 1] [1, 1, 1, 1, 1] [1, 0, 0, 0, 1]
Algorithm
Let’s first define the test input:
test = [2,1,0,1]
After this, we will apply the naive bayes algorithm:
probYes = 1
count = 0
total = 0
for row in dataset:
if(row[-1] == 1):
count+=1
total+=1
print("Total yes: "+str(count)+" / "+str(total))
probYes *= count/total
for i in range(len(test)):
count = 0
total = 0
for row in mp[1]:
if(test[i] == row[i]):
count += 1
total += 1
print('for feature '+str(i+1))
print(str(count)+" / "+str(total))
probYes *= count/total
probNo = 1
count = 0
total = 0
for row in dataset:
if(row[-1] == 0):
count+=1
total+=1
probNo *= count/total
print("Total no: "+str(count)+" / "+str(total))
for i in range(len(test)):
count = 0
total = 0
for row in mp[0]:
if(test[i] == row[i]):
count += 1
total += 1
print('for feature '+str(i+1))
print(str(count)+" / "+str(total))
probNo *= count/totalTotal yes: 9 / 14 for feature 1 3 / 9 for feature 2 4 / 9 for feature 3 6 / 9 for feature 4 3 / 9 Total no: 5 / 14 for feature 1 2 / 5 for feature 2 2 / 5 for feature 3 1 / 5 for feature 4 3 / 5
Let’s print the probability of playing golf and not playing golf:
print(probYes) print(probNo)
0.021164021164021163 0.006857142857142859
Calculating the probability of playing golf
To calculate the probability of playing golf, we will use the following code:
prob = probYes/(probYes+probNo)
print("Probability of playing golf: "+str(prob*100)+"%")Probability of playing golf: 75.5287009063444%
That’s it. The probability of playing golf will be calculated according to the previous data using naive bayes algorithm.
Complete code
dataset = [
[0,0,1,0,0],
[0,0,1,1,0],
[1,0,1,0,1],
[2,1,1,0,1],
[2,2,0,0,1],
[2,2,0,1,0],
[1,2,0,1,1],
[0,1,1,0,0],
[0,2,0,0,1],
[2,1,0,0,1],
[0,1,0,1,1],
[1,1,1,1,1],
[1,0,0,0,1],
[2,1,1,1,0]
]
mp = dict()
for i in range(len(dataset)):
row = dataset[i]
y = row[-1]
if (y not in mp):
mp[y] = list()
mp[y].append(row)
for label in mp:
print(label)
for row in mp[label]:
print(row)
test = [2,1,0,1]
probYes = 1
count = 0
total = 0
for row in dataset:
if(row[-1] == 1):
count+=1
total+=1
print("Total yes: "+str(count)+" / "+str(total))
probYes *= count/total
for i in range(len(test)):
count = 0
total = 0
for row in mp[1]:
if(test[i] == row[i]):
count += 1
total += 1
print('for feature '+str(i+1))
print(str(count)+" / "+str(total))
probYes *= count/total
probNo = 1
count = 0
total = 0
for row in dataset:
if(row[-1] == 0):
count+=1
total+=1
probNo *= count/total
print("Total no: "+str(count)+" / "+str(total))
for i in range(len(test)):
count = 0
total = 0
for row in mp[0]:
if(test[i] == row[i]):
count += 1
total += 1
print('for feature '+str(i+1))
print(str(count)+" / "+str(total))
probNo *= count/total
print(probYes)
print(probNo)
prob = probYes/(probYes+probNo)
print("Probability of playing golf: "+str(prob*100)+"%")Other Machine Learning algorithms:
- Naive Bayes Classification
- K Nearest Neighbors
- Linear Regression
- K Means Clustering
- Apriori Algorithm
- Principal Component Analysis (PCA)
Let us know in the comments if you are having any questions regarding this machine learning algorithm.
And if you found this post helpful, then please help us by sharing this post with your friends. Thank You

